 KOI 2011 지역본선 책장
KOI 2011 지역본선 책장
Problem https://www.acmicpc.net/problem/2466 Summary N 개의 책이 주어진다.각 책 마다 너비 W 와 높이 H 가 주어지고, 주어진 순서대로 책장에 꽂으려 한다. 모든 책을 꽂기 위한 책장의 너비와 높이중 최대값을 최소로 하려고 할 때, 그 최소값은 얼마일까? Solution 너비와 높이 중 최대값을 최소로 하는 문제이다.모든 책을 꽂아야 하는 책장의 특성상 너비가 증가함에 따라 높이가 단조감소하고, 너비가 줄어들면 높이가 단조증가하게 된다.따라서 책장의 너비(폭) 을 고정시키고, 그 때의 최소 높이를 구한 다음 그 높이를 기준으로 책장의 너비를 늘릴지 줄일지 결정할 수 있고 따라서 이 문제는 파라메트릭 서치로 접근 가능하다. 그렇다면 책장의 너비를 고정 시켰을 ..
우선 K=1일때에는 트리의 지름에 설치하는것이 가장최적이라는 결론을 내릴수 있는데 그에 대한 증명을 위해서 지름길을 설치했을때의 경로길이를 수식으로 표현해보자 일단 지름길을 설치하지 않았을때에는 모든간선을 2번씩 지나야함으로 경로이길이는 2(N-1)이 된다. 지름길을 하나 설치하면 트리에 간선을 하나 추가하는 행위임으로 반드시 하나의 사이클이 생기게된다.이때 사이클 위에 존재하는 간선은 한번씩만 사이클위에 속하지 않는 간선은 2번씩지나야함으로경로의 길이는 2(N-1) - L + 1이 되는데 L은 (사이클 위에 포함된 정점의 갯수-1)개 이다. 따라서 K=1일때는 간선을 추가하여 만드는 사이클의 길이(즉, 정점갯수-1) 가 최대가 되게 하면 됨으로 트리에 지름에 설치하는것이 가장 최적이라는 결과가 나온다...
그래프 에서매칭 = 변집합 로, 상호 끝점을 공유하지 않는다.변 덮개 = 변집합 로, 의 어떤 정점도 적어도 1개의 에 포함된 변에 접속 하고 있다.안정집합 = 점집합 로, 의 어떤 두점도 에 대해 인접하고 있지 않다.점 덮개 = 점집합 로, 의 어떤 변도 적어도 1개의 에 포함된 정점에 접속하고 있다.일때 몇가지 법칙이 성립한다. 1. 고립점이 없는 그래프에서 대해서, |최대매칭| + |최소 변 덮개| = |V|2. |최대 안정 집합| + |최소 점 덮개| = |V| 특히 이분그래프에서는|최대 매칭| = |최소 변 덮개| 가 된다. http://prague.algospot.com/judge/problem/read/TRAPCARD위 문제가 위의 성질을 이용하여 풀수있는 대표적인 문제이다이문제는 갯수만 출..
 다이나믹 -- 시작복잡도 줄이기
다이나믹 -- 시작복잡도 줄이기
dynamic programming 문제들중 와 같은 점화식을 가진 문제들에 대해 생각해보자. 실제로 최근 KOI에서도 위와 같은 점화식을 가진 문제가 몇몇 나왔는데2011 전국 중등부3 번이라던가2011 지역 고등부5 번을 예로 들 수 있다. 위와 같은 점화식을 가진 문제는 특수한 경우에 따라 시간복잡도를 에서 으로 바꿔 풀 수 있다. 1. commando (APIO 2010)위 문제의 점화식을 나타내보면여기서 bX항은 그룹을 어떻게 나누는지에는 상관없이 항상 그 값은 과 같게 된다.따라서 위 점화식을 로 두고 마지막에 b*(x1+x2..+xn) 을 더해주면 위와같은 점화식이 된다는것을 확인할 수 있다. 그리고 c는 j값에 상관없이 항상 일정한 값을 가지기 때문에우리는 고정된 i 에 대하여 의 값을만에..
링크 : http://211.228.163.31/pool/coci_traka/coci_traka.php?pname=coci_traka Solution 1) O(NM) D(j) = j번째 사람이 첫번째 작업을 시작할 최소시간 이라 정의하자. 그러면 모든 i에 대하여 D(j) + {T(1)+T(2)+T(3)...+T(i)}*F(j) = D(j) + {T(1)+T(2)+T(3)...+T(i-1)}{F(j)-F(j+1)} + T(i)*F(j) 가 성립해야한다. 즉 D(j+1) = D(j) + max( {T(1)+T(2)+T(3)...+T(i-1)}{F(j)-F(j+1)} + T(i)*F(j) ) 라는 식을 얻어낼수 있다. 따라서 모든j에 대해서 모든 i를 훑으면, O(NM)솔루션을 얻어낼수 있다. 2) O(Nl..
 Hanoi Tower
Hanoi Tower
http://211.228.163.31/30stair/hanoi1/hanoi1.php?pname=hanoi1 문제를 요약하자면 현재상태의 하노이 탑이 주어졌을때 1,2,3번 기둥중 어떤기둥으로 옮기는지는 상관없고, 최소의 이동으로 모든 조각을 한곳에 모을때 최소이동과 어디로 모으는 것이 최적인지 구하는것이다. 일단 이문제는 linear 하게 풀릴수 있다. 가장 쉽게 떠올릴수 있는 방법이 모든 경우를 다해보는 backtracking 기법인데. 이문제의 실제 N범위가 100,000인걸 감안한다면 으론 해결할수 없다. 그렇다면 어떻게 접근해야 풀수 있을까? 1) 우선 우리는 N개의 하노이를 한 기둥에서 다른기둥으로 옮기기 위해 이동해야하는 최소횟수는 임이 자명하다. 2) 그리고 우리가 최종적으로 옮겨야할 목적..
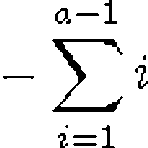 I'm coder 2nd!!
I'm coder 2nd!!
오랜만에 글써보내요 다름이 아니라 최근에 참가한 모의고사에 대한 풀이를 올려볼까 합니다. 결과페이지 : http://www.koistudy.net/bbs/moi/2nd/result.php 저는 대회때 1,2번을 풀고 3,4번을 고민하다가 결국 몇점 받지도 못했네요 ㅋㅋ 1. Sum (http://koistudy.net/?mid=prob_page&NO=502) 일단 두가지 방법으로 접근이 가능한것 같습니다. 첫번째 방법) 우선 인 모든 a,b의 쌍을 찾아내는것이 문제입니다. 위 식을 다음과같이 정리하면 즉 가 됩니다. 다시말해 시작점을 정해버리면 끝점은 만에 구해낼수 있다는것이죠 ! 따라서 으로 모든 시작점을 고려하면 됩니다. 두번째 방법) 두번째 방법으로는 범위를 늘렸다 줄였다 하는 Sliding win..
헤르메스의 심부름그리스 신들이 사는 현대식 도시에는 길거리의 도로들이 X, Y 축에 평행하며 정수 좌표로 된 격자 형태로 배열되어 있다. 임의의 정수 Z에 대해, y=Z로 표현되는 수평 도로가 있고, x=Z로 표현되는 수직 도로가 있다. 그래서 정수로 구성된 좌표는 수평· 수직 도로가 만나는 교차로가 된다. 날씨가 더우면 신들은 바로 이 교차로들 중 어디엔가 있는 카페테리아에 따로 따로 흩어져 쉰다. 신들의 심부름꾼인 헤르메스는 이날도 길거리의 도로만 이용하여 이동한 뒤, 여러 카페테리아에 흩어져 있는 신들에게 메시지를 부지런히 전달한다. 한 메시지는 한 신만을 대상으로 하고 있으나, 전달 과정에서 메시지가 다른 신이 있는 지점을 통과하더라도 상관은 없다. 헤르메스는 초기에 원점 (0, 0)에 있다. 전..
